纽约长岛有着漫长的海岸线，石溪大学坐拥一片自己的私人海滩。这片海滩藏在密林深处，不为人知。虽然时有狂风暴雪，惊涛骇浪，但更多时候还是海空一色，天地澄明。潮汐日复一日地冲刷，将岸边的砾石打磨得浑圆润泽。有一片海滩上遍布石英鹅卵石，浸润在海水中，在阳光照耀下玲珑剔透，晶莹透明。大海中生活着神秘的物种，有着活化石之称的马蹄蟹，戴着坦克般的铠甲在海边游弋。亿万年的岁月没有带给马蹄蟹丝毫的进化，大洋中的生态也是亘古不变。阵阵海风掠过，带来大海新鲜而苦涩的气息，层层叠叠的海浪散落在沙滩上，留下雪白的泡沫和翠绿的海藻。成群的海鸥展翅迎风，鸣叫着悬停在浪尖之上。似乎在这里，时光永驻，岁月静好。多少代人看到的是同样的晨昏景致，听到的是同样的天籁涛声，苍茫而荒凉，古老而悠远。但是波澜不兴的大洋表面之下，时刻暗流涌动，酝酿着时代巨变。

超越时代

上个世纪七十年代初期的一天，一位年轻的化学系助理教授和他三岁的女儿在海滨散步。小女孩目光非常敏锐，在岸边捡到了一只幼小的黑色蛤蜊，直径不到半厘米。深夜，父亲返回实验室，将蛤蜊放入一只细长的试管，再将试管注满重水，放入自己搭建的简陋仪器。他在机器轰鸣声中采集了数据，然后用笨重的计算器来进行繁冗的计算。人类历史上第一张活体断层图像诞生了！年轻教授匆匆写就论文投向了《自然》期刊。

不幸的是论文惨遭拒稿，《自然》编辑的理由是图像过于模糊。年轻教授奋起抗争，他向编委控诉道：“过去50年的科学历史可以由《Science》或《Nature》的拒稿来写就！” 编委被其诚意打动，经过谨慎的重审之后接收了这篇划时代的论文。但是，石溪大学拒绝为这项发明申请专利，专家们一致认为“这项发明可能带来的转让费不会弥补专利申请费。”

那个时候，石溪有一位年轻的数学系教授同样面临着不为人理解的困局。石溪数学系一直是北美几何重镇，很多资深教授在学界享有盛誉。他们研究黎曼几何的手法倚重比较定理。例如给定两条边长和夹角，平面三角形的第三条边长大于球面三角形的第三条边长。年轻人认为这种陈旧的手法过于粗糙，精密程度远远低于偏微分方程。但是在那个年代，偏微分方程和几何是两个相距甚远的分支学科，资深教授不相信年轻人离经叛道的言论。年轻人毅然决然地开始了将偏微分方程和微分几何相融合的历程。

这两位年轻人超越了他们所处的时代，他们没有摧眉折腰地盲从主流，而是大无畏地追求理想。最终，石溪大学因为自身的短视和保守失去了这两位年轻才俊。这位数学家是丘成桐先生，他融合了偏微分方程和微分几何，创立了几何分析学派，于1982年荣获菲尔兹奖。那位化学家是Paul Lauterbur博士，他因为发明了核磁共振断层扫描技术于2003年获得诺贝尔医学奖。

一片蓝海

2003年，老顾和学生们来到了同一片海滩，风景依旧，但是革命正在发生。那时核磁共振技术正在为医学领域带来一场深刻的变革。人类可以轻而易举地获取各种器官图像，但是如何精确分析这些器官的几何形状和纹理特征成为学术领域的研究热点。由此催生了一个新兴领域，医学图像处理。一个比较基本的问题在于如何建立两张拓扑复杂曲面间映射，使得映射光滑可逆，满足一些特征点的对应关系，即找到曲面间带限制条件的微分同胚。比如为了监控奥兹海默症的发展，我们需要定量测量大脑皮层曲面的萎缩程度，因此需要建立大脑皮层曲面间的微分同胚，逐点比较时隔一年扫描的同一个大脑皮层。这一问题被称为“曲面注册”问题。曲面注册可以用调和映照来解决。所谓调和映照可以如下直观解释：我们将源曲面看成是橡皮膜，罩在目标曲面上自由滑动，假设摩擦力为0，最后系统平衡时，曲面弹性形变能量最小，所得映射即为调和映照。

老顾和学生们经常在海边讨论这些几何理论和工程问题，老顾逐渐看到了眼前的一片蓝海：用丘成桐先生开创的几何分析理论做Lauterbur博士开创的医学图像问题。

在十数年的漫长岁月，调和映照方法已经在医学图像领域广泛使用。通过回顾这段历史，老顾对于数学研究和计算机科学发展之间的关系有了切身体会。现代社会分工日益精细，每个人的知识结构、专业技能愈发狭窄。数学理论因为形式化和严格化的要求，非常晦涩难解。数学家和计算机科学家之间的直接交流相对困难。目前的计算机科学专业训练依然达不到理解几何分析的初级理论的阶段，数学家也很少有机会能够判断他们发展的理论是否有实用价值。但是时代的发展需要这两的学术方向的深度融合。基于多年的观察，老顾对于这方面的很多问题形成了自己的见解。下面，我们以调和映照与曲面注册问题的关系，来回答这些问题。

1.拓扑圆盘的调和映照。

灵感来源

1. 实用算法的发明是否需要艰深的数学理论？

在医学图像处理中，我们经常需要将单连通的曲面映射到平面上面，如图（1）所示。任何一个具备初步计算机图形学、或者视觉的本科生都可以自己设计并实现这一算法。其灵感来自于童年的物理世界中的真实游戏。

图2. 三角网格的数据结构。

计算机中几何曲面被表示成离散的三角网格，如图（2）所示。我们将每条边看成一条弹簧，每个顶点看成一个粒子，弹簧弹性形变的能量为弹性系数和延长量平方的乘积。如图（1）所示，我们将边界均匀固定在圆周上，在平衡状态时，整个系统的弹性形变势能最小，这就给出了调和映射。因此，算法归结为优化弹性形变能量：

简单的算法给出相对满意的结果。

但是相应的调和映照理论却非常艰深。首先，给定两个带黎曼度量的曲面和一个光滑映射

，我们选取等温坐标系，

映射的调和能量为

调和映照是极小化调和能量的映射，从而满足下面的欧拉-拉格朗日方程：

从理论上，我们需要证明解的存在性，解的唯一性，解的光滑性，以及解是否是微分同胚。这些证明需要概念、技巧和方法需要多年的数学专业训练才能掌握，对于计算机编程并没有直接帮助。但是，如果你追踪这些数学技巧的内在灵感来源，依然是童年的物理世界中的游戏，特别是小男孩热衷的那些破坏性游戏。

比如理论中最为曲折的存在性证明依循如下思路。经典函数空间对极限运算并不封闭，我们需要将其添加一些广义函数，拓展成索伯列夫空间。在索伯列夫空间中找到一个序列极小化调和能量，那么可以证明这一序列在索伯列夫空间中收敛，但是有可能收敛到一个广义映射。我需要进一步证明，如此得到的极限是古典解，即连续映射。这一步的关键是用调和能量对连续模进行估计，需要用到库朗-勒贝格引理。这个引理描述了这样一个破坏性试验：我们撕裂一个气球，得到一片橡皮膜，用力拉伸将其形变，形变后的周长取决于初始周长和弹性形变能量的大小。如果我们将橡皮膜的边界拉扯到圆周上，保证边界处没有皱褶，那么橡皮膜会均匀地绷在圆盘上，内部也没有皱褶；如果我们将橡皮膜的边界拉扯到平面非凸多边形上，那么橡皮膜内部可能出现皱褶，但是整个橡皮膜落在边界的凸包（convex hull）内部。这些游戏经验实际上正是证明调和映照存在性的关键观察。因此，比较淘气的男生应该容易理解掌握。现代小孩逐渐脱离现实物理世界，沉湎于虚拟游戏，对于以后几何、拓扑学的学习会有负面影响。

到目前为止，似乎调和映照理论用艰涩的语言，严密地陈述了一些肤浅的日常经验，对于算法的设计与提升没有起到实质性的帮助。另一方面，在程序的调试过程中，我们发现极为重要的计算稳定性和计算效率问题。这些问题超出了日常经验，也不在调和映照理论关心的范畴。

稳定性和效率

2. 使得一个算法真正实用的关键在哪里？

求解调和映照等价于优化调和能量，从理论上讲，调和能量的凸性决定了算法的稳定性。优化的方法主要有一阶近似的梯度下降法，和二阶近似的牛顿法，牛顿法的效率远高于梯度下降法。在实际计算中，微分算子被矩阵表示，牛顿法归结为大型对称正定稀疏矩阵求解。在数值代数中，人们发明了多种算法来求解线性系统，比如常用的共轭梯度法等等。这些迭代算法的数值稳定性和收敛速度取决于矩阵的条件数。而条件数最后归结为曲面三角剖分的质量。

给定光滑曲面构造高质量的三角剖分，这是网格生成领域的核心问题。上个世纪70年代开始，计算几何领域开始创立。基于Delaunay三角剖分，Voronoi图的算法被大量发明出来。基于Delaunay三角剖分的网格生成目前是工业界的主流，但是高维网格生成，弯曲流形的三角剖分依然没有发展成熟。光滑流形的离散逼近理论在本世纪初期开始日渐成熟，主要是基于微分几何的离散法丛理论。这一领域依然在蓬勃发展，存在大量尚未解决的基础问题。

众所周知，基本的几何计算，例如一个点在三角形内部或者外部，在计算机上是极不稳定的，这依赖于CPU的硬件实现。虽然理论上不值一哂，但是这个貌似平庸的问题在实践中是致命的。这也是为什么很多美轮美奂的算法，实际上无法实用的核心原因之一。为了提高数值稳定性，人们又发明了复杂的算法予以保证。

数值代数，计算几何，计算代数，网格生成，这些新兴领域都是因为计算机的兴起，响应时代呼唤而发展起来的交叉学科。虽然抽象程度不及基础理论，但是它们在应用中不可或缺。

理论指导

3. 深刻几何理论对于实用算法的指导作用体现在哪里？是否是不可或缺？

从上述讨论中，我们得到如此印象：似乎物理直观加上工程技巧可以应对实际情况，那么是否有必要钻研深刻抽象的理论呢？对此，老顾的学生们都曾发生过困惑。直到我们遇到大脑皮层映射问题。

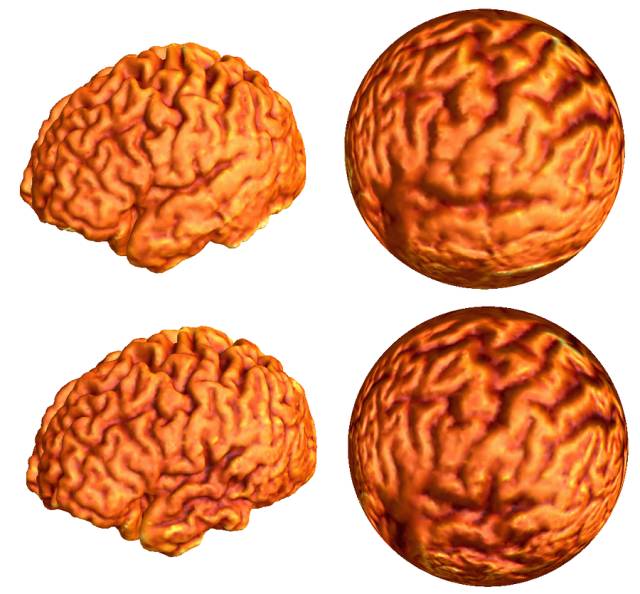
图3. 共形脑图。

如图（3）所示，我们希望比较两张大脑皮层曲面，一种方法是将它们映射到单位球面上，然后在球面上进行比对。在实践中，我们发现在工程方面相对完美之后，经过长时间的调试，调和映照的算法依然不稳定。

真正的根源解释来自调和映照理论。首先拓扑球面间的调和映照必是共形映射，其次球面到自身的共形映射不唯一，构成一个6维的莫比乌斯变换群。因此调和映照的算法无法收敛到某一个解，在映照空间中震荡。如此，我们可以添加一些限制条件，使得解唯一，例如令重心和原点重合以去除莫比乌斯歧义性等等。

这些理论结果在日常生活中非常难以直接观察到，凭借简单的经验已经无法对数值实验的不稳定性给出合理解释，必须引入几何理论中的深刻结果来对实践加以指导。

图4. 带特征点的曲面注册问题。每个小圆被映到相应的椭圆。

又如图（4）所示的带特征点曲面注册问题。给定一些对应的特征点，我们欲求取微分同胚。如果直接用带限制的调和映射来计算，所得结果非产生皱褶，而非同胚。这样的缺陷并非来自工程误差，而是来自理论层面的限制。丘先生曾经证明过一个定理：如果目标曲面的黎曼度量诱导的高斯曲率处处为负，那么度为一的调和映射必然是微分同胚。这里用到Bochner公式，将黎曼度量、高斯曲率、调和映照的雅克比矩阵联系起来。由此，我们得到启发：将目标曲面的黎曼度量换成负曲率度量，再计算调和映照。但是我们遇到了巨大的障碍，在那个年代，计算数学领域、计算机科学领域没有任何实用方法可以数值构造黎曼度量。我们只能求助于几何分析理论。

二十世纪初，庞加莱奠定了代数拓扑的基础，提出了著名的庞加莱猜想：单连通的三维紧流形和三维球面拓扑同胚。证明这一猜想成为拓扑学家梦寐以求的目标。虽然这个猜想是拓扑的，其最终证明却是用几何分析的方法。在1982年哈密尔顿提出了黎奇流的纲领来证明庞加莱猜想：

在二十一世纪初，黎奇流方法成功地证明了庞加莱猜想。黎奇流成为了用曲率来构造度量的强有力的理论工具。老顾和合作者们花费了十数年，建立了离散黎奇流的理论和算法，从而可以自如地构造各种黎曼度量。

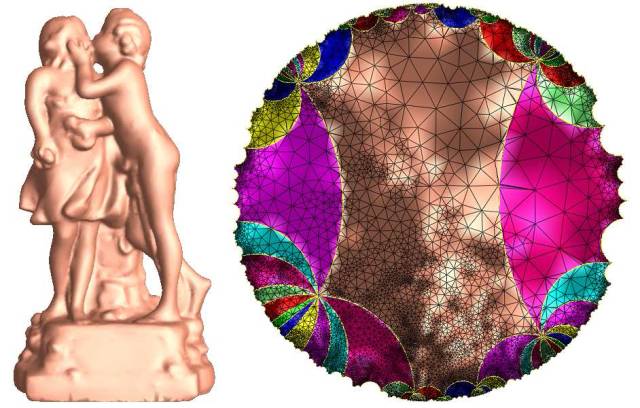
图5. 离散黎奇流得到的双曲度量。

有了双曲度量之后，我们可以将图（4）中的曲面去掉特征点，然后配上双曲度量，在双曲度量下计算调和映照，得到微分同胚。在这种情形下，给定两个同伦映射，我们可以用测地线来连接对应点，从而在映射空间中构造一个变分。由于目标空间曲率为负，我们可以保证调和能量沿着变分是凸函数，因此每一同伦类中调和映射唯一。从而保证了算法的稳定性。

从抽象的庞加莱猜想到实际的三维人脸比对，这期间的道路过于漫长，这显示了抽象数学的普适性和基础性。图（5）双曲度量远离日常生活经验，因为左侧的曲面配上双曲度量后在现实的三维空间中无法实现。人类仅凭经验和直觉是无法领悟出丘成桐先生的定理。如果对调和映照理论没有深刻的理解，这种算法是无法提出并实现的。

实践对理论的反作用

4. 计算机科学是被动地从几何理论中汲取营养？还是对基础科学也有推动作用？

依随对调和映照理论和算法的深入理解，我们逐渐发现调和映照对于处理非流形空间依然卓有成效。特别是，在最近新兴的等几何分析（isogeometric analysis）中，调和映照起到了核心作用。等几何分析需要实体被结构化六面体剖分，构造这种剖分的关键是得到边界曲面上的叶状结构。叶状结构被建筑大师哈迪德（Zaha Hadid）广泛应用于她所设计的地标性建筑。

图6. Galaxy - Soho 建筑表面的叶状结构 （Zaha Hadid Architecture）。

计算曲面上的叶状结构等价于求解从曲面到某种一维复形（Graph图）的调和映照。从计算机算法角度而言，将曲面间的调和映照算法修改成叶状结构算法非常直接了当，但是从数学理论角度而言，两者之间存在一条难以逾越的天堑。

图7. 曲面上的叶状结构。

由于目标不再是光滑流形，传统的微分几何工具无法直接应用。索伯列夫空间、调和能量、曲率这一切都要重新定义。虽然几何实质相近，但是将这些直觉严密化有着本质的困难。丘先生的弟子 Richard Schoen完成了这一壮举，从而为这一优美的算法奠定了坚实的理论基础。同样，我们发展的离散曲面黎奇流理论，也可以用于证明经典的曲面单值化定理。

小结

回顾这段亲身历史，我们看到几何分析理论和计算机科学之间的关系。粗浅的算法可以基于直觉而发展出来，发展到深入阶段之后，需要仰仗抽象深刻的数学来指导，日常经验已经无能为力。基础理论转化成实用算法，存在很多实际的困难需要解决，由此衍生了诸多交叉学科。同时，工程实践也推动了基础理论从连续流形到离散空间的发展。

从调和映照理论到曲面匹配算法，社会分工的链条非常漫长，每一个环节都足以耗尽一个学者的生命。老顾认识很多数学家，看到他们对于偏微分方程的每一项都有着无法与人尽述的感觉和深情；也认识网格生成领域的领军人物，看到他数十年来对于三角剖分无比痴迷；同时看到应用领域的青年才俊为了打造一个软件系统，夜以继日，废寝忘食。每个领域都有内在的魅力和挑战，都是时代发展不可或缺的环节。基础理论比较艰辛，需要多年的积累，在人类文明金字塔顶，具有恒久的价值；应用科学成才迅速，推动时代发展，具有现实意义。数学更加美丽，计算机更加有力。

暴雪过后，老顾和学生们又会来到石溪海滩。2018年的春天，他们谈论最多的是深度学习的理论解释，最优传输理论、蒙日-安培方程的几何图景 。。。